Medical practitioners frequently encounter patients with vaccine hesitancy, which is the delay in acceptance or refusal of vaccination despite availability of vaccination services.1,2 A recent study found while 8% of parents did not complete the National Immunisation Program Schedule for their children, an additional 44% reported varying levels of concern despite completing the schedule.2 This shows how vaccine acceptance does not necessarily indicate the absence of hesitancy, and understanding the mathematical basis behind immunisation scheduling may help address these concerns.3,1
Patients who are knowledgeable about community-level protection, known as ‘herd immunity’, are more likely to be positive about vaccination.4 However, some internet forums refer to herd immunity as a myth, wrongly criticising its lack of scientific evidence and questioning its basis.5 For those with such concerns, introducing the mathematical foundations of herd immunity, which guide national vaccination strategies, may provide a valuable tool for addressing these questions. Considering that fact that the vast majority of parents are most influenced by the information obtained from their general practitioner (GP) about vaccinations, such interactions may provide a valuable opportunity for this.2
Explaining how vaccinations work using mathematics
To calculate herd immunity, mathematicians typically divide people into three groups: susceptible (S), infectious (I) and removed (R). To be categorised into the R group, people need to have achieved immunity by either natural infection or vaccination. Therefore, the spread of infection depends on the proportion of susceptible and infectious individuals in a population, as the R group cannot be infected.6 If the R group is sufficiently large, infection cannot spread, and the population is said to have herd immunity protecting those at risk of infection. The number of people required to be in the R group is based on the infectivity of a disease, expressed in a quantity called the basic reproduction number (R0). The quantity R0 is equal to the average number of individuals that one infectious person infects in a wholly susceptible population. For example, if R0 is less than one, this signifies that each infectious person will infect less than one susceptible person, and thus infection will not spread. Thus, the optimum size of the R group is that which reduces R0 to less than one.
| Table 1. Examples of the basic reproduction number (R0) for some common vaccine targets including influenza virus (‘the flu’), varicella-zoster virus (chickenpox) and measles virus, rounded to one decimal place. R0 denotes the number of people infected by one infectious person in a susceptible population. |
| Infective agent |
Number of people infected by one
infectious person |
R0 |
| Salmonella7 |
Less than one person |
0.8 |
| Influenza8 |
1.3 people |
1.3 |
| Varicella zoster7 |
8.5 people |
8.5 |
| Measles9 |
17 people |
17 |
Table 1 shows the values of R0 for some common vaccine-preventable diseases,
with a higher R0 equating to diseases that are more infective. From these values of R0, the proportion of people needed in the R group to prevent spread of infection can be calculated using the equation:
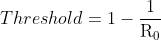
For example, as shown in Table 1, measles has a basic reproduction number of 17; one infected person produces 17 new infections in a totally susceptible population. By substituting 17 for R0, the equation becomes:
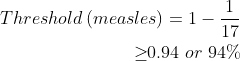
In short, at least 94% of the population needs to be in the R group (ie previously infected or vaccinated) for the R0 of measles to become less than one and thus prevent spread of the disease. This explains why the Australian measles herd immunity target has been set at approximately 95% for the population.10
On the other hand, the basic reproduction number for influenza is approximately 1.3 (Table 1), resulting in a lower threshold to achieve herd immunity:
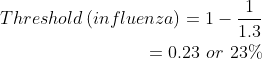
This shows that measles is more difficult to control by vaccination than the flu because measles has a much higher R0.
A simple example like this may not only explain to a hesitant patient why vaccination against measles is more important than vaccination against influenza, but also quantify to the patient the potential individual impact of vaccine refusal. Preventing the infection of 17 people with measles gives a patient a clearer idea of the importance of individual vaccination than simply discussing general community benefit from vaccination in a non-quantitative way.
Importantly, it should be noted these calculations do not only apply to the national level but also to a community population to prevent local outbreaks. Thus, the size of a disease outbreak can be estimated on the basis of the R0 of a disease and also the proportion vaccinated in a local community.
For example, North Sydney, New South Wales (NSW), currently has a 91% childhood immunisation rate for measles.11 If this translated into 91% of the population being immune, in the event of a measles outbreak, an estimated 3% of the local population would be infected before reaching the herd immunity threshold (94%).
Alternatively, if there was a measles outbreak in Nimbin, NSW, where childhood immunisation rates are as low as 40%, potentially up to 54% of the population may be infected before achieving the herd immunity threshold and protecting the remaining 6% of population susceptible to infection.11
The Australian public health approach is to control the spread of disease by maintaining populations at the disease-specific herd immunity threshold to prevent epidemics. The spread of disease is related to the proportion of infectious, susceptible and recovered individuals in the population at a given time. An important limitation of this work is that the infectivity of a disease, as captured in R0, is not related to the consequences of infection. Therefore, while influenza has a lower R0 than measles, it is just as important to vaccinate, as influenza infection can also be lethal. Understanding the basis of herd immunity can provide a useful tool for GPs, as part of a multi-faceted approach, to help their patients better understand the importance of vaccination for the local population and address vaccination hesitancy.
Readers interested in a more extensive history and explanation of the mathematics are directed to Mathematic epidemiology: Past, present, and future by Brauer (2017).6